Regression

In this notebook we demonstrate how to fit a Gaussian process regression model.

# Enable Float64 for more stable matrix inversions.
from jax import config
import jax.numpy as jnp
import jax.random as jr
from jaxtyping import install_import_hook
import matplotlib as mpl
import matplotlib.pyplot as plt

from examples.utils import (
    clean_legend,
    use_mpl_style,
)

config.update("jax_enable_x64", True)


with install_import_hook("gpjax", "beartype.beartype"):
    import gpjax as gpx


key = jr.key(123)

# set the default style for plotting
use_mpl_style()

cols = mpl.rcParams["axes.prop_cycle"].by_key()["color"]

Dataset

With the necessary modules imported, we simulate a dataset $\mathcal{D} = (\boldsymbol{x}, \boldsymbol{y}) = \{(x_i, y_i)\}_{i=1}^{100}$ with inputs $\boldsymbol{x}$ sampled uniformly on $(-3., 3)$ and corresponding independent noisy outputs

\[\boldsymbol{y} \sim \mathcal{N} \left(\sin(4\boldsymbol{x}) + \cos(2 \boldsymbol{x}), \textbf{I} * 0.3^2 \right).\]

We store our data $\mathcal{D}$ as a GPJax Dataset and create test inputs and labels for later.

n = 100
noise = 0.3

key, subkey = jr.split(key)
x = jr.uniform(key=key, minval=-3.0, maxval=3.0, shape=(n,)).reshape(-1, 1)
f = lambda x: jnp.sin(4 * x) + jnp.cos(2 * x)
signal = f(x)
y = signal + jr.normal(subkey, shape=signal.shape) * noise

D = gpx.Dataset(X=x, y=y)

xtest = jnp.linspace(-3.5, 3.5, 500).reshape(-1, 1)
ytest = f(xtest)

To better understand what we have simulated, we plot both the underlying latent function and the observed data that is subject to Gaussian noise.

fig, ax = plt.subplots()
ax.plot(x, y, "o", label="Observations", color=cols[0])
ax.plot(xtest, ytest, label="Latent function", color=cols[1])
ax.legend(loc="best")

<matplotlib.legend.Legend at 0x7fe6548ae500>

png

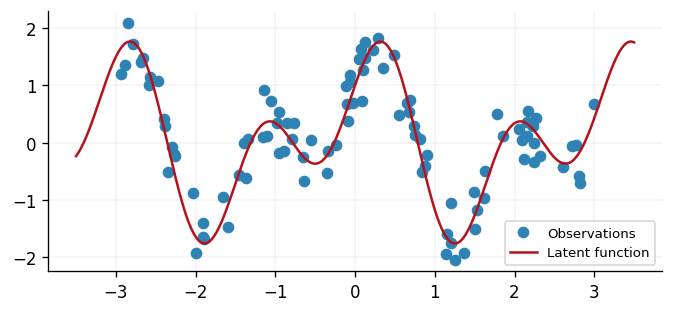
Our aim in this tutorial will be to reconstruct the latent function from our noisy observations $\mathcal{D}$ via Gaussian process regression. We begin by defining a Gaussian process prior in the next section.

Defining the prior

A zero-mean Gaussian process (GP) places a prior distribution over real-valued functions $f(\cdot)$ where $f(\boldsymbol{x}) \sim \mathcal{N}(0, \mathbf{K}_{\boldsymbol{x}\boldsymbol{x}})$ for any finite collection of inputs $\boldsymbol{x}$.

Here $\mathbf{K}_{\boldsymbol{x}\boldsymbol{x}}$ is the Gram matrix generated by a user-specified symmetric, non-negative definite kernel function $k(\cdot, \cdot')$ with $[\mathbf{K}_{\boldsymbol{x}\boldsymbol{x}}]_{i, j} = k(x_i, x_j)$. The choice of kernel function is critical as, among other things, it governs the smoothness of the outputs that our GP can generate.

For simplicity, we consider a radial basis function (RBF) kernel:

\[k(x, x') = \sigma^2 \exp\left(-\frac{\lVert x - x' \rVert_2^2}{2 \ell^2}\right).\]

On paper a GP is written as $f(\cdot) \sim \mathcal{GP}(\textbf{0}, k(\cdot, \cdot'))$, we can reciprocate this process in GPJax via defining a Prior with our chosen RBF kernel.

kernel = gpx.kernels.RBF()  # 1-dimensional input
meanf = gpx.mean_functions.Zero()
prior = gpx.gps.Prior(mean_function=meanf, kernel=kernel)

The above construction forms the foundation for GPJax's models. Moreover, the GP prior we have just defined can be represented by a TensorFlow Probability multivariate Gaussian distribution. Such functionality enables trivial sampling, and the evaluation of the GP's mean and covariance .

prior_dist = prior.predict(xtest)

prior_mean = prior_dist.mean()
prior_std = prior_dist.variance()
samples = prior_dist.sample(seed=key, sample_shape=(20,))


fig, ax = plt.subplots()
ax.plot(xtest, samples.T, alpha=0.5, color=cols[0], label="Prior samples")
ax.plot(xtest, prior_mean, color=cols[1], label="Prior mean")
ax.fill_between(
    xtest.flatten(),
    prior_mean - prior_std,
    prior_mean + prior_std,
    alpha=0.3,
    color=cols[1],
    label="Prior variance",
)
ax.legend(loc="best")
ax = clean_legend(ax)

png

Constructing the posterior

Having defined our GP, we proceed to define a description of our data $\mathcal{D}$ conditional on our knowledge of $f(\cdot)$ --- this is exactly the notion of a likelihood function $p(\mathcal{D} | f(\cdot))$. While the choice of likelihood is a critical in Bayesian modelling, for simplicity we consider a Gaussian with noise parameter $\alpha$

\[p(\mathcal{D} | f(\cdot)) = \mathcal{N}(\boldsymbol{y}; f(\boldsymbol{x}), \textbf{I} \alpha^2).\]

This is defined in GPJax through calling a Gaussian instance.

likelihood = gpx.likelihoods.Gaussian(num_datapoints=D.n)

The posterior is proportional to the prior multiplied by the likelihood, written as

$$ p(f(\cdot) | \mathcal{D}) \propto p(f(\cdot)) * p(\mathcal{D} | f(\cdot)). $$

Mimicking this construct, the posterior is established in GPJax through the * operator.

posterior = prior * likelihood

Parameter state

As outlined in the PyTrees documentation, parameters are contained within the model and for the leaves of the PyTree. Consequently, in this particular model, we have three parameters: the kernel lengthscale, kernel variance and the observation noise variance. Whilst we have initialised each of these to 1, we can learn Type 2 MLEs for each of these parameters by optimising the marginal log-likelihood (MLL).

print(-gpx.objectives.conjugate_mll(posterior, D))

124.80517341248417

We can now define an optimiser. For this example we'll use the bfgs optimiser.

opt_posterior, history = gpx.fit_scipy(
    model=posterior,
    # we use the negative mll as we are minimising
    objective=lambda p, d: -gpx.objectives.conjugate_mll(p, d),
    train_data=D,
)

print(-gpx.objectives.conjugate_mll(opt_posterior, D))

Optimization terminated successfully.
         Current function value: 55.074053
         Iterations: 16
         Function evaluations: 19
         Gradient evaluations: 19
55.07405321945008

Prediction

Equipped with the posterior and a set of optimised hyperparameter values, we are now in a position to query our GP's predictive distribution at novel test inputs. To do this, we use our defined posterior and likelihood at our test inputs to obtain the predictive distribution as a Distrax multivariate Gaussian upon which mean and stddev can be used to extract the predictive mean and standard deviatation.

latent_dist = opt_posterior.predict(xtest, train_data=D)
predictive_dist = opt_posterior.likelihood(latent_dist)

predictive_mean = predictive_dist.mean()
predictive_std = predictive_dist.stddev()

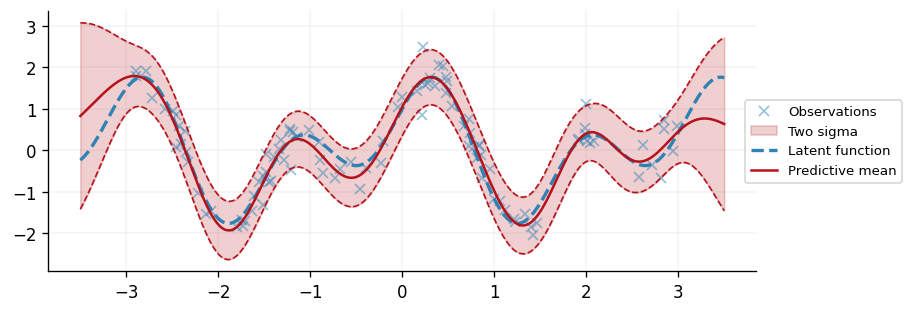
With the predictions and their uncertainty acquired, we illustrate the GP's performance at explaining the data $\mathcal{D}$ and recovering the underlying latent function of interest.

fig, ax = plt.subplots(figsize=(7.5, 2.5))
ax.plot(x, y, "x", label="Observations", color=cols[0], alpha=0.5)
ax.fill_between(
    xtest.squeeze(),
    predictive_mean - 2 * predictive_std,
    predictive_mean + 2 * predictive_std,
    alpha=0.2,
    label="Two sigma",
    color=cols[1],
)
ax.plot(
    xtest,
    predictive_mean - 2 * predictive_std,
    linestyle="--",
    linewidth=1,
    color=cols[1],
)
ax.plot(
    xtest,
    predictive_mean + 2 * predictive_std,
    linestyle="--",
    linewidth=1,
    color=cols[1],
)
ax.plot(
    xtest, ytest, label="Latent function", color=cols[0], linestyle="--", linewidth=2
)
ax.plot(xtest, predictive_mean, label="Predictive mean", color=cols[1])
ax.legend(loc="center left", bbox_to_anchor=(0.975, 0.5))

<matplotlib.legend.Legend at 0x7fe64c9e9b10>

png

System configuration

%reload_ext watermark
%watermark -n -u -v -iv -w -a 'Thomas Pinder & Daniel Dodd'

Author: Thomas Pinder & Daniel Dodd

Last updated: Fri Nov 01 2024

Python implementation: CPython
Python version       : 3.10.15
IPython version      : 8.29.0

jax       : 0.4.27
matplotlib: 3.9.2
gpjax     : 0.9.3
jaxtyping : 0.2.34

Watermark: 2.5.0