Sparse Stochastic Variational Inference

In this notebook we demonstrate how to implement sparse variational Gaussian processes (SVGPs) of Hensman et al. (2015). In particular, this approximation framework provides a tractable option for working with non-conjugate Gaussian processes with more than ~5000 data points. However, for conjugate models of less than 5000 data points, we recommend using the marginal log-likelihood approach presented in the regression notebook. Though we illustrate SVGPs here with a conjugate regression example, the same GPJax code works for general likelihoods, such as a Bernoulli for classification.

# Enable Float64 for more stable matrix inversions.
from jax import config
import jax.numpy as jnp
import jax.random as jr
from jaxtyping import install_import_hook
import matplotlib as mpl
import matplotlib.pyplot as plt
import optax as ox

from examples.utils import use_mpl_style

config.update("jax_enable_x64", True)


with install_import_hook("gpjax", "beartype.beartype"):
    import gpjax as gpx
    import gpjax.kernels as jk

key = jr.key(123)

# set the default style for plotting
use_mpl_style()
cols = mpl.rcParams["axes.prop_cycle"].by_key()["color"]

Dataset

With the necessary modules imported, we simulate a dataset $\mathcal{D} = (\boldsymbol{x}, \boldsymbol{y}) = \{(x_i, y_i)\}_{i=1}^{5000}$ with inputs $\boldsymbol{x}$ sampled uniformly on $(-5, 5)$ and corresponding binary outputs

$$\boldsymbol{y} \sim \mathcal{N} \left(\sin(4 * \boldsymbol{x}) + \sin(2 * \boldsymbol{x}), \textbf{I} * (0.2)^{2} \right).$$

We store our data $\mathcal{D}$ as a GPJax Dataset and create test inputs for later.

n = 50000
noise = 0.2

key, subkey = jr.split(key)
x = jr.uniform(key=key, minval=-5.0, maxval=5.0, shape=(n,)).reshape(-1, 1)
f = lambda x: jnp.sin(4 * x) + jnp.cos(2 * x)
signal = f(x)
y = signal + jr.normal(subkey, shape=signal.shape) * noise
D = gpx.Dataset(X=x, y=y)

xtest = jnp.linspace(-5.5, 5.5, 500).reshape(-1, 1)

Sparse GPs via inducing inputs

Despite their endowment with elegant theoretical properties, GPs are burdened with prohibitive $\mathcal{O}(n^3)$ inference and $\mathcal{O}(n^2)$ memory costs in the number of data points $n$ due to the necessity of computing inverses and determinants of the kernel Gram matrix $\mathbf{K}_{\boldsymbol{x}\boldsymbol{x}}$ during inference and hyperparameter learning. Sparse GPs seek to resolve tractability through low-rank approximations.

Their name originates with the idea of using subsets of the data to approximate the kernel matrix, with sparseness occurring through the selection of the data points. Given inputs $\boldsymbol{x}$ and outputs $\boldsymbol{y}$ the task was to select an $m<n$ lower-dimensional dataset $(\boldsymbol{z},\boldsymbol{\tilde{y}}) \subset (\boldsymbol{x}, \boldsymbol{y})$ to train a Gaussian process on instead. By generalising the set of selected points $\boldsymbol{z}$, known as inducing inputs, to remove the restriction of being part of the dataset, we can arrive at a flexible low-rank approximation framework of the model using functions of $\mathbf{K}_{\boldsymbol{z}\boldsymbol{z}}$ to replace the true covariance matrix $\mathbf{K}_{\boldsymbol{x}\boldsymbol{x}}$ at significantly lower costs. For example, review many popular approximation schemes in this vein. However, because the model and the approximation are intertwined, assigning performance and faults to one or the other becomes tricky.

On the other hand, sparse variational Gaussian processes (SVGPs) approximate the posterior, not the model. These provide a low-rank approximation scheme via variational inference. Here we posit a family of densities parameterised by "variational parameters". We then seek to find the closest family member to the posterior by minimising the Kullback-Leibler divergence over the variational parameters. The fitted variational density then serves as a proxy for the exact posterior. This procedure makes variational methods efficiently solvable via off-the-shelf optimisation techniques whilst retaining the true-underlying model. Furthermore, SVGPs offer further cost reductions with mini-batch stochastic gradient descent and address non-conjugacy . We show a cost comparison between the approaches below, where $b$ is the mini-batch size.

	GPs	sparse GPs	SVGP
Inference cost	$\mathcal{O}(n^3)$	$\mathcal{O}(n m^2)$	$\mathcal{O}(b m^2 + m^3)$
Memory cost	$\mathcal{O}(n^2)$	$\mathcal{O}(n m)$	$\mathcal{O}(b m + m^2)$

To apply SVGP inference to our dataset, we begin by initialising $m = 50$ equally spaced inducing inputs $\boldsymbol{z}$ across our observed data's support. These are depicted below via horizontal black lines.

z = jnp.linspace(-5.0, 5.0, 50).reshape(-1, 1)

fig, ax = plt.subplots()
ax.vlines(
    z,
    ymin=y.min(),
    ymax=y.max(),
    alpha=0.3,
    linewidth=1,
    label="Inducing point",
    color=cols[2],
)
ax.scatter(x, y, alpha=0.2, color=cols[0], label="Observations")
ax.plot(xtest, f(xtest), color=cols[1], label="Latent function")
ax.legend()
ax.set(xlabel=r"$x$", ylabel=r"$f(x)$")

[Text(0.5, 0, '$x$'), Text(0, 0.5, '$f(x)$')]

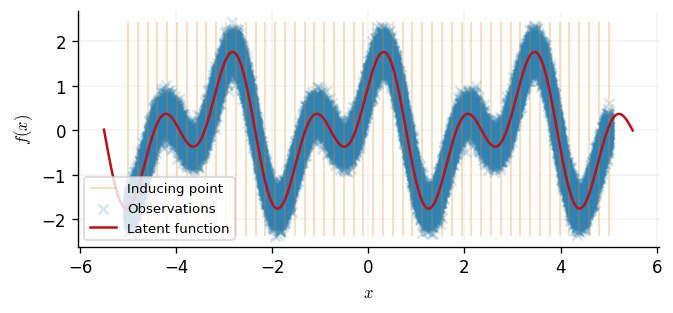
The inducing inputs will summarise our dataset, and since they are treated as variational parameters, their locations will be optimised. The next step to SVGP is to define a variational family.

Defining the variational process

We begin by considering the form of the posterior distribution for all function values $f(\cdot)$

$$\begin{align} p(f(\cdot) | \mathcal{D}) = \int p(f(\cdot)|f(\boldsymbol{x})) p(f(\boldsymbol{x})|\mathcal{D}) \text{d}f(\boldsymbol{x}). \qquad (\dagger) \end{align}$$

To arrive at an approximation framework, we assume some redundancy in the data. Instead of predicting $f(\cdot)$ with function values at the datapoints $f(\boldsymbol{x})$, we assume this can be achieved with only function values at $m$ inducing inputs $\boldsymbol{z}$

$$p(f(\cdot) | \mathcal{D}) \approx \int p(f(\cdot)|f(\boldsymbol{z})) p(f(\boldsymbol{z})|\mathcal{D}) \text{d}f(\boldsymbol{z}). \qquad (\star)$$

This lower dimensional integral results in computational savings in the model's predictive component from $p(f(\cdot)|f(\boldsymbol{x}))$ to $p(f(\cdot)|f(\boldsymbol{z}))$ where inverting $\mathbf{K}_{\boldsymbol{x}\boldsymbol{x}}$ is replaced with inverting $\mathbf{K}_{\boldsymbol{z}\boldsymbol{z}}$. However, since we did not observe our data $\mathcal{D}$ at $\boldsymbol{z}$ we ask, what exactly is the posterior $p(f(\boldsymbol{z})|\mathcal{D})$?

Notice this is simply obtained by substituting $\boldsymbol{z}$ into $(\dagger)$, but we arrive back at square one with computing the expensive integral. To side-step this, we consider replacing $p(f(\boldsymbol{z})|\mathcal{D})$ in $(\star)$ with a cheap-to-compute approximate distribution $q(f(\boldsymbol{z}))$

$$q(f(\cdot)) = \int p(f(\cdot)|f(\boldsymbol{z})) q(f(\boldsymbol{z})) \text{d}f(\boldsymbol{z}). \qquad (\times)$$

To measure the quality of the approximation, we consider the Kullback-Leibler divergence $\operatorname{KL}(\cdot || \cdot)$ from our approximate process $q(f(\cdot))$ to the true process $p(f(\cdot)|\mathcal{D})$. By parametrising $q(f(\boldsymbol{z}))$ over a variational family of distributions, we can optimise Kullback-Leibler divergence with respect to the variational parameters. Moreover, since inducing input locations $\boldsymbol{z}$ augment the model, they themselves can be treated as variational parameters without altering the true underlying model $p(f(\boldsymbol{z})|\mathcal{D})$. This is exactly what gives SVGPs great flexibility whilst retaining robustness to overfitting.

It is popular to elect a Gaussian variational distribution $q(f(\boldsymbol{z})) = \mathcal{N}(f(\boldsymbol{z}); \mathbf{m}, \mathbf{S})$ with parameters $\{\boldsymbol{z}, \mathbf{m}, \mathbf{S}\}$, since conjugacy is provided between $q(f(\boldsymbol{z}))$ and $p(f(\cdot)|f(\boldsymbol{z}))$ so that the resulting variational process $q(f(\cdot))$ is a GP. We can implement this in GPJax by the following.

meanf = gpx.mean_functions.Zero()
likelihood = gpx.likelihoods.Gaussian(num_datapoints=n)
kernel = jk.RBF()  # 1-dimensional inputs
prior = gpx.gps.Prior(mean_function=meanf, kernel=kernel)
p = prior * likelihood
q = gpx.variational_families.VariationalGaussian(posterior=p, inducing_inputs=z)

Here, the variational process $q(\cdot)$ depends on the prior through $p(f(\cdot)|f(\boldsymbol{z}))$ in $(\times)$.

Inference

Evidence lower bound

With our model defined, we seek to infer the optimal inducing inputs $\boldsymbol{z}$, variational mean $\mathbf{m}$ and covariance $\mathbf{S}$ that define our approximate posterior. To achieve this, we maximise the evidence lower bound (ELBO) with respect to $\{\boldsymbol{z}, \mathbf{m}, \mathbf{S} \}$, a proxy for minimising the Kullback-Leibler divergence. Moreover, as hinted by its name, the ELBO is a lower bound to the marginal log-likelihood, providing a tractable objective to optimise the model's hyperparameters akin to the conjugate setting. For further details on this, see Sections 3.1 and 4.1 of the excellent review paper .

Mini-batching

Despite introducing inducing inputs into our model, inference can still be intractable with large datasets. To circumvent this, optimisation can be done using stochastic mini-batches.

schedule = ox.warmup_cosine_decay_schedule(
    init_value=0.0,
    peak_value=0.02,
    warmup_steps=75,
    decay_steps=2000,
    end_value=0.001,
)

opt_posterior, history = gpx.fit(
    model=q,
    # we are minimizing the elbo so we negate it
    objective=lambda p, d: -gpx.objectives.elbo(p, d),
    train_data=D,
    optim=ox.adam(learning_rate=schedule),
    num_iters=3000,
    key=jr.key(42),
    batch_size=128,
)

  0%|          | 0/3000 [00:00<?, ?it/s]

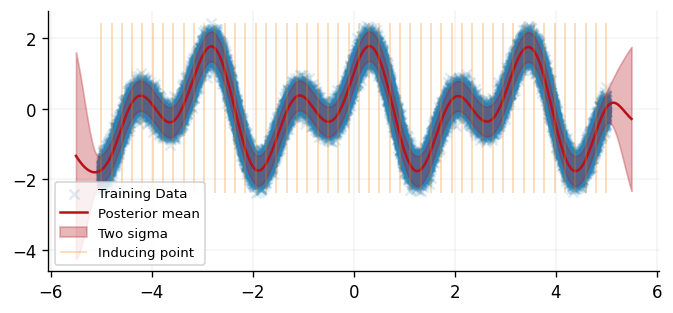
Predictions

With optimisation complete, we can use our inferred parameter set to make predictions at novel inputs akin to all other models within GPJax on our variational process object $q(\cdot)$ (for example, see the regression notebook).

latent_dist = opt_posterior(xtest)
predictive_dist = opt_posterior.posterior.likelihood(latent_dist)

meanf = predictive_dist.mean
sigma = jnp.sqrt(predictive_dist.variance)

fig, ax = plt.subplots()
ax.scatter(x, y, alpha=0.15, label="Training Data", color=cols[0])
ax.plot(xtest, meanf, label="Posterior mean", color=cols[1])
ax.fill_between(
    xtest.flatten(),
    meanf - 2 * sigma,
    meanf + 2 * sigma,
    alpha=0.3,
    color=cols[1],
    label="Two sigma",
)
ax.vlines(
    opt_posterior.inducing_inputs.value,
    ymin=y.min(),
    ymax=y.max(),
    alpha=0.3,
    linewidth=1,
    label="Inducing point",
    color=cols[2],
)
ax.legend()

<matplotlib.legend.Legend at 0x7fc174f84e80>

System configuration

%reload_ext watermark
%watermark -n -u -v -iv -w -a 'Thomas Pinder, Daniel Dodd & Zeel B Patel'

Author: Thomas Pinder, Daniel Dodd & Zeel B Patel

Last updated: Tue May 20 2025

Python implementation: CPython
Python version       : 3.10.16
IPython version      : 8.36.0

jaxtyping : 0.3.2
optax     : 0.2.4
gpjax     : 0.11.1
jax       : 0.6.0
matplotlib: 3.10.3

Watermark: 2.5.0