Deep Kernel Learning
In this notebook we demonstrate how GPJax can be used in conjunction with Flax to build deep kernel Gaussian processes. Modelling data with discontinuities is a challenging task for regular Gaussian process models. However, as shown in , transforming the inputs to our Gaussian process model's kernel through a neural network can offer a solution to this.
from dataclasses import (
dataclass,
field,
)
from flax import nnx
import jax
# Enable Float64 for more stable matrix inversions.
from jax import config
import jax.numpy as jnp
import jax.random as jr
from jaxtyping import (
Array,
Float,
install_import_hook,
)
import matplotlib as mpl
import matplotlib.pyplot as plt
import optax as ox
from scipy.signal import sawtooth
from examples.utils import use_mpl_style
from gpjax.kernels.computations import (
AbstractKernelComputation,
DenseKernelComputation,
)
config.update("jax_enable_x64", True)
with install_import_hook("gpjax", "beartype.beartype"):
import gpjax as gpx
from gpjax.kernels.base import AbstractKernel
from gpjax.parameters import (
Parameter,
)
# set the default style for plotting
use_mpl_style()
cols = mpl.rcParams["axes.prop_cycle"].by_key()["color"]
key = jr.key(42)
Dataset
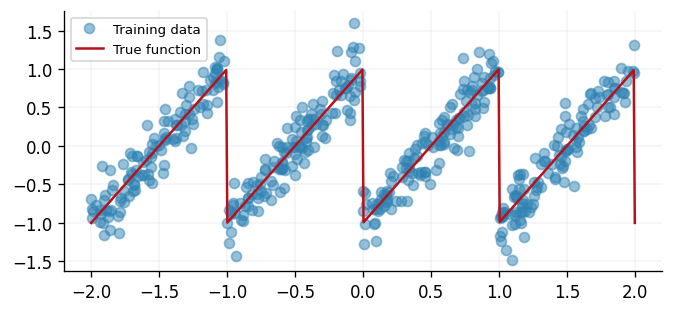
As previously mentioned, deep kernels are particularly useful when the data has discontinuities. To highlight this, we will use a sawtooth function as our data.
n = 500
noise = 0.2
key, subkey = jr.split(key)
x = jr.uniform(key=key, minval=-2.0, maxval=2.0, shape=(n,)).reshape(-1, 1)
f = lambda x: jnp.asarray(sawtooth(2 * jnp.pi * x))
signal = f(x)
y = signal + jr.normal(subkey, shape=signal.shape) * noise
D = gpx.Dataset(X=x, y=y)
xtest = jnp.linspace(-2.0, 2.0, 500).reshape(-1, 1)
ytest = f(xtest)
fig, ax = plt.subplots()
ax.plot(x, y, "o", label="Training data", alpha=0.5)
ax.plot(xtest, ytest, label="True function")
ax.legend(loc="best")
<matplotlib.legend.Legend at 0x7fa1ec773c50>
Deep kernels
Details
Instead of applying a kernel directly on some data, we seek to apply a feature map that projects the data to learn more meaningful representations beforehand. In deep kernel learning, is a neural network whose parameters are learned jointly with the GP model's hyperparameters. The corresponding kernel is then computed by . Here is referred to as the base kernel.
Implementation
Although deep kernels are not currently supported natively in GPJax, defining one is
straightforward as we now demonstrate. Inheriting from the base AbstractKernel
in GPJax, we create the DeepKernelFunction object that allows the
user to supply the neural network and base kernel of their choice. Kernel matrices
are then computed using the regular gram and cross_covariance functions.
@dataclass
class DeepKernelFunction(AbstractKernel):
base_kernel: AbstractKernel
network: nnx.Module
compute_engine: AbstractKernelComputation = field(
default_factory=lambda: DenseKernelComputation()
)
def __call__(
self, x: Float[Array, " D"], y: Float[Array, " D"]
) -> Float[Array, "1"]:
xt = self.network(x)
yt = self.network(y)
return self.base_kernel(xt, yt)
Defining a network
With a deep kernel object created, we proceed to define a neural network. Here we consider a small multi-layer perceptron with two linear hidden layers and ReLU activation functions between the layers. The first hidden layer contains 64 units, while the second layer contains 32 units. Finally, we'll make the output of our network a three units wide. The corresponding kernel that we define will then be of ARD form to allow for different lengthscales in each dimension of the feature space. Users may wish to design more intricate network structures for more complex tasks, which functionality is supported well in Haiku.
feature_space_dim = 3
class Network(nnx.Module):
def __init__(
self, rngs: nnx.Rngs, *, input_dim: int, inner_dim: int, feature_space_dim: int
) -> None:
self.layer1 = nnx.Linear(input_dim, inner_dim, rngs=rngs)
self.output_layer = nnx.Linear(inner_dim, feature_space_dim, rngs=rngs)
self.rngs = rngs
def __call__(self, x: jax.Array) -> jax.Array:
x = x.reshape((x.shape[0], -1))
x = self.layer1(x)
x = jax.nn.relu(x)
x = self.output_layer(x).squeeze()
return x
forward_linear = Network(
nnx.Rngs(123), feature_space_dim=feature_space_dim, inner_dim=32, input_dim=1
)
Defining a model
Having characterised the feature extraction network, we move to define a Gaussian process parameterised by this deep kernel. We consider a third-order Matérn base kernel and assume a Gaussian likelihood.
base_kernel = gpx.kernels.Matern52(
active_dims=list(range(feature_space_dim)),
lengthscale=jnp.ones((feature_space_dim,)),
)
kernel = DeepKernelFunction(network=forward_linear, base_kernel=base_kernel)
meanf = gpx.mean_functions.Zero()
prior = gpx.gps.Prior(mean_function=meanf, kernel=kernel)
likelihood = gpx.likelihoods.Gaussian(num_datapoints=D.n)
posterior = prior * likelihood
Optimisation
We train our model via maximum likelihood estimation of the marginal log-likelihood. The parameters of our neural network are learned jointly with the model's hyperparameter set.
With the inclusion of a neural network, we take this opportunity to highlight the additional benefits gleaned from using Optax for optimisation. In particular, we showcase the ability to use a learning rate scheduler that decays the optimiser's learning rate throughout the inference. We decrease the learning rate according to a half-cosine curve over 700 iterations, providing us with large step sizes early in the optimisation procedure before approaching more conservative values, ensuring we do not step too far. We also consider a linear warmup, where the learning rate is increased from 0 to 1 over 50 steps to get a reasonable initial learning rate value.
schedule = ox.warmup_cosine_decay_schedule(
init_value=0.0,
peak_value=0.01,
warmup_steps=75,
decay_steps=700,
end_value=0.0,
)
optimiser = ox.chain(
ox.clip(1.0),
ox.adamw(learning_rate=schedule),
)
# Train all parameters (default behavior with trainable=Parameter)
# Alternative options for selective training:
# - trainable=PositiveReal # only train positive parameters
# - trainable=lambda module, path, value: 'kernel' in path # only kernel params
opt_posterior, history = gpx.fit(
model=posterior,
objective=lambda p, d: -gpx.objectives.conjugate_mll(p, d),
train_data=D,
optim=optimiser,
num_iters=800,
key=key,
trainable=Parameter, # explicitly specify trainable filter (default)
)
0%| | 0/800 [00:00<?, ?it/s]
Prediction
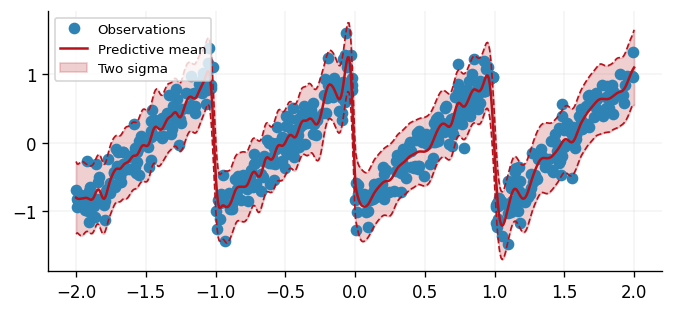
With a set of learned parameters, the only remaining task is to predict the output of the model. We can do this by simply applying the model to a test data set.
latent_dist = opt_posterior(xtest, train_data=D)
predictive_dist = opt_posterior.likelihood(latent_dist)
predictive_mean = predictive_dist.mean
predictive_std = jnp.sqrt(predictive_dist.variance)
fig, ax = plt.subplots()
ax.plot(x, y, "o", label="Observations", color=cols[0])
ax.plot(xtest, predictive_mean, label="Predictive mean", color=cols[1])
ax.fill_between(
xtest.squeeze(),
predictive_mean - 2 * predictive_std,
predictive_mean + 2 * predictive_std,
alpha=0.2,
color=cols[1],
label="Two sigma",
)
ax.plot(
xtest,
predictive_mean - 2 * predictive_std,
color=cols[1],
linestyle="--",
linewidth=1,
)
ax.plot(
xtest,
predictive_mean + 2 * predictive_std,
color=cols[1],
linestyle="--",
linewidth=1,
)
ax.legend()
<matplotlib.legend.Legend at 0x7fa1c8a5f210>
System configuration
Author: Thomas Pinder
Last updated: Mon Dec 15 2025
Python implementation: CPython
Python version : 3.11.14
IPython version : 9.5.0
optax : 0.2.5
gpjax : 0.13.4
jax : 0.7.1
jaxtyping : 0.3.2
scipy : 1.16.1
flax : 0.12.0
matplotlib: 3.10.6
Watermark: 2.5.0