Orthogonal Additive Kernels
In this notebook we demonstrate the Orthogonal Additive Kernel (OAK) of Lu, Boukouvalas & Hensman (2022). OAK provides an interpretable additive Gaussian process model that decomposes the target function into main effects and interaction terms, whilst remaining a valid positive-definite kernel. The key ingredients are:
- A per-dimension constrained SE kernel that is orthogonal to the constant function under the input density.
- Newton-Girard recursion to efficiently combine these constrained kernels into elementary symmetric polynomials up to a chosen interaction order.
- Analytic Sobol indices that quantify the relative importance of each interaction order, enabling practitioners to understand which features and feature interactions drive the model's predictions.
We illustrate the full workflow on the UCI Auto MPG dataset.
# Enable Float64 for more stable matrix inversions.
from jax import config
config.update("jax_enable_x64", True)
from examples.utils import use_mpl_style
import jax.numpy as jnp
import jax.random as jr
from jaxtyping import install_import_hook
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
with install_import_hook("gpjax", "beartype.beartype"):
import gpjax as gpx
from gpjax.kernels.additive import (
OrthogonalAdditiveKernel,
predict_first_order,
rank_first_order,
sobol_indices,
)
from gpjax.parameters import Parameter
key = jr.key(123)
use_mpl_style()
colours = mpl.rcParams["axes.prop_cycle"].by_key()["color"]
Mathematical background
Additive GP decomposition
A standard GP with a single kernel \(k(\mathbf{x}, \mathbf{x}')\) treats all input dimensions jointly. An additive GP instead decomposes the latent function as
where \(f_0\) is a constant offset, \(f_d\) are first-order (main) effects, \(f_{dd'}\) are second-order interactions, and so on. Truncating at a maximum interaction order \(\tilde{D} \le D\) yields a model that scales gracefully whilst retaining interpretability.
The identifiability problem
A naive additive decomposition is unidentifiable: one can freely shift mass between the constant term and a main effect, or between a main effect and an interaction. Lu et al. resolve this by requiring each component to be orthogonal to all lower-order components under the input density \(p(\mathbf{x})\). In particular, the first-order components satisfy
Constrained SE kernel
Assuming a standard normal input density \(p(x_d) = \mathcal{N}(0, 1)\), the orthogonality constraint can be enforced analytically. The constrained SE kernel is
where \(k(x,y) = \sigma^2 \exp\!\bigl(-\tfrac{(x-y)^2}{2\ell^2}\bigr)\) is the standard SE kernel with lengthscale \(\ell\) and variance \(\sigma^2\). The subtracted projection term removes the component of \(k\) that lies along the constant function under the \(\mathcal{N}(0,1)\) measure.
Newton-Girard recursion
The additive kernel across all interaction orders up to \(\tilde{D}\) is
where \(e_\ell\) denotes the \(\ell\)-th elementary symmetric polynomial and \(\sigma_\ell^2\) are learnable order variances. Computing \(e_\ell\) directly via the combinatorial definition would be prohibitively expensive; instead GPJax uses the Newton-Girard identities which express \(e_\ell\) recursively in terms of power sums \(s_k = \sum_{d=1}^D z_d^k\):
Sobol indices
Once the model is fitted, the relative importance of each interaction order can be quantified via Sobol indices. The Sobol index for order \(d\) is
where \(\boldsymbol{\alpha} = (K + \sigma_n^2 I)^{-1}\mathbf{y}\) and \(E_d\) is the matrix-level elementary symmetric polynomial of the per-dimension integral matrices (see Appendix G.1 of the paper).
Dataset
We use the UCI Auto MPG dataset, which contains fuel consumption data for 392 cars described by 7 continuous features (cylinders, displacement, horsepower, weight, acceleration, model year, and origin).
Because the OAK kernel's constrained form assumes a standard normal input density (\(\mu = 0\), \(\sigma^2 = 1\)), we fit a per-feature normalising flow that maps each marginal to an approximately standard normal distribution. Targets are z-score standardised. This transformation of the inputs data is crucial for the OAK model to work correctly, as the orthogonality constraint is defined with respect to the input density.
from ucimlrepo import fetch_ucirepo
auto_mpg = fetch_ucirepo(id=9)
X_raw = auto_mpg.data.features
y_raw = auto_mpg.data.targets
# Drop rows with missing values
complete_rows = ~(X_raw.isna().any(axis=1) | y_raw.isna().any(axis=1))
X_all = X_raw[complete_rows].values.astype(np.float64)
y_all = y_raw[complete_rows].values.astype(np.float64)
feature_names = list(X_raw.columns)
num_features = X_all.shape[1]
print(f"Dataset: {X_all.shape[0]} observations, {num_features} features")
print(f"Features: {feature_names}")
Dataset: 392 observations, 7 features
Features: ['displacement', 'cylinders', 'horsepower', 'weight', 'acceleration', 'model_year', 'origin']
Normalising flow and train/test split
The constrained SE kernel assumes \(p(x_d) = \mathcal{N}(0,1)\). Simple z-scoring removes the first two moments but cannot correct skewness or heavy tails. We therefore fit a lightweight per-feature normalising flow (Shift → Log → Standardise → SinhArcsinh) that maps each marginal to an approximately standard normal distribution.
y_mean, y_std = y_all.mean(axis=0), y_all.std(axis=0)
y_standardised = (y_all - y_mean) / y_std
num_observations = y_standardised.shape[0]
key, split_key = jr.split(key)
permutation = jr.permutation(split_key, num_observations)
num_train = int(0.8 * num_observations)
train_idx = permutation[:num_train]
test_idx = permutation[num_train:]
y_train = jnp.array(y_standardised[train_idx])
y_test = jnp.array(y_standardised[test_idx])
X_train_original = X_all[train_idx]
X_test_original = X_all[test_idx]
flows = fit_all_normalising_flows(jnp.asarray(X_train_original))
def apply_flows(X_original: np.ndarray) -> jnp.ndarray:
"""Transform each feature column through its fitted normalising flow."""
return jnp.column_stack(
[flows[d](jnp.asarray(X_original[:, d])) for d in range(num_features)]
)
X_train = apply_flows(X_train_original)
X_test = apply_flows(X_test_original)
train_data = gpx.Dataset(X=X_train, y=y_train)
test_data = gpx.Dataset(X=X_test, y=y_test)
Fitting an OAK GP
We create \(D\) independent RBF base kernels, one per input dimension, each
operating on a single dimension via active_dims=[i]. These are wrapped
inside OrthogonalAdditiveKernel with max_order=D (i.e. we allow all
interaction orders). The kernel is then used in a standard conjugate GP
workflow: define a prior and Gaussian likelihood, form the posterior, and
optimise hyperparameters by maximising the marginal log-likelihood.
base_kernels = [gpx.kernels.RBF(active_dims=[i]) for i in range(num_features)]
oak_kernel = OrthogonalAdditiveKernel(base_kernels, max_order=3)
mean_function = gpx.mean_functions.Zero()
prior = gpx.gps.Prior(mean_function=mean_function, kernel=oak_kernel)
likelihood = gpx.likelihoods.Gaussian(num_datapoints=num_train)
posterior = prior * likelihood
negative_mll = lambda posterior, data: -gpx.objectives.conjugate_mll(posterior, data)
opt_posterior, history = gpx.fit_scipy(
model=posterior,
objective=negative_mll,
train_data=train_data,
trainable=Parameter,
)
latent_dist = opt_posterior.predict(
X_test, train_data=train_data, return_covariance_type="diagonal"
)
predictive_dist = opt_posterior.likelihood(latent_dist)
predictive_mean = predictive_dist.mean
Optimization terminated successfully.
Current function value: 107.174483
Iterations: 56
Function evaluations: 60
Gradient evaluations: 60
Sobol indices
We now compute the analytic Sobol indices for each interaction order. These indicate what fraction of the posterior variance is explained by first-order (main) effects, second-order interactions, and so on.
noise_variance = float(jnp.square(opt_posterior.likelihood.obs_stddev[...]))
fitted_kernel = opt_posterior.prior.kernel
sobol_values = sobol_indices(fitted_kernel, X_train, y_train, noise_variance)
fig, ax = plt.subplots(figsize=(7, 3))
orders = jnp.arange(1, len(sobol_values) + 1)
ax.bar(orders, sobol_values, color=colours[1])
ax.set_xlabel("Interaction order")
ax.set_ylabel("Sobol index")
ax.set_title("Sobol indices by interaction order")
ax.set_xticks(np.arange(1, len(sobol_values) + 1))
[<matplotlib.axis.XTick at 0x7fed91f8f150>,
<matplotlib.axis.XTick at 0x7fed9097eb50>,
<matplotlib.axis.XTick at 0x7fed93597390>]
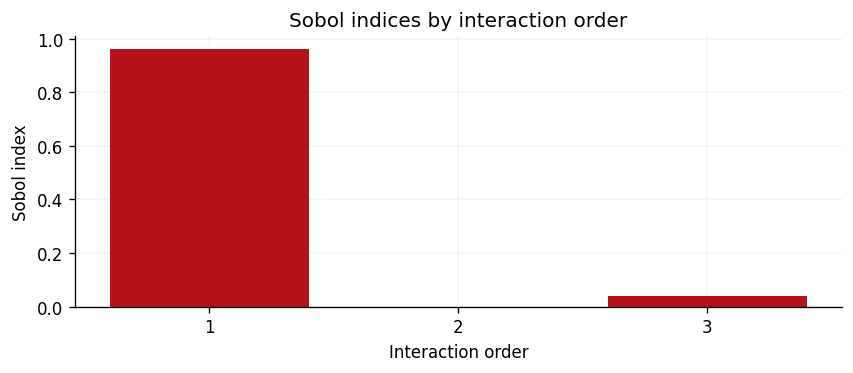
Typically the first-order (main) effects dominate, with higher-order interactions contributing progressively less. This validates the additive modelling assumption for this dataset.
Decomposed additive components
One of the key advantages of the OAK model is the ability to visualise each feature's individual contribution to the prediction. We extract the top 4 first-order main effects and plot the posterior mean and a \(\pm 2\sigma\) credible band for each, alongside a histogram of the training inputs.
For each feature \(d\), we evaluate the constrained kernel \(\tilde{k}_d(x_*, X_{\mathrm{train},d})\) between a 1-D grid and the training points, then form the conditional mean and variance in the usual GP way.
num_top_features = 3
num_grid_points = 300
feature_scores = rank_first_order(fitted_kernel, X_train, y_train, noise_variance)
top_feature_indices = jnp.argsort(-feature_scores)[:num_top_features]
fig, axes = plt.subplots(nrows=1, ncols=num_top_features, figsize=(12, 3))
for plot_idx, ax in enumerate(axes.flat):
feature_dim = int(top_feature_indices[plot_idx])
feature_name = feature_names[feature_dim]
grid_low = float(X_train[:, feature_dim].min())
grid_high = float(X_train[:, feature_dim].max())
grid = jnp.linspace(grid_low, grid_high, num_grid_points)
effect_mean, effect_variance = predict_first_order(
fitted_kernel, X_train, y_train, noise_variance, feature_dim, grid
)
effect_std = jnp.sqrt(effect_variance)
grid_original_scale = flows[feature_dim].inv(grid)
ax.plot(
grid_original_scale,
effect_mean,
color=colours[1],
linewidth=2,
label="Posterior mean",
)
ax.fill_between(
grid_original_scale,
effect_mean - 2 * effect_std,
effect_mean + 2 * effect_std,
alpha=0.2,
color=colours[1],
label=r"$\pm 2\sigma$",
)
histogram_ax = ax.twinx()
histogram_ax.hist(
X_train_original[:, feature_dim],
bins=20,
alpha=0.15,
color=colours[0],
density=True,
)
histogram_ax.set_yticks([])
ax.set_xlabel(feature_name)
ax.set_ylabel("Effect")
ax.set_title(f"{feature_name} (dim {feature_dim})")
ax.legend(loc="best", fontsize=8)
fig.suptitle(f"Top {num_top_features} first-order main effects", fontsize=14, y=1.05)
Text(0.5, 1.05, 'Top 3 first-order main effects')
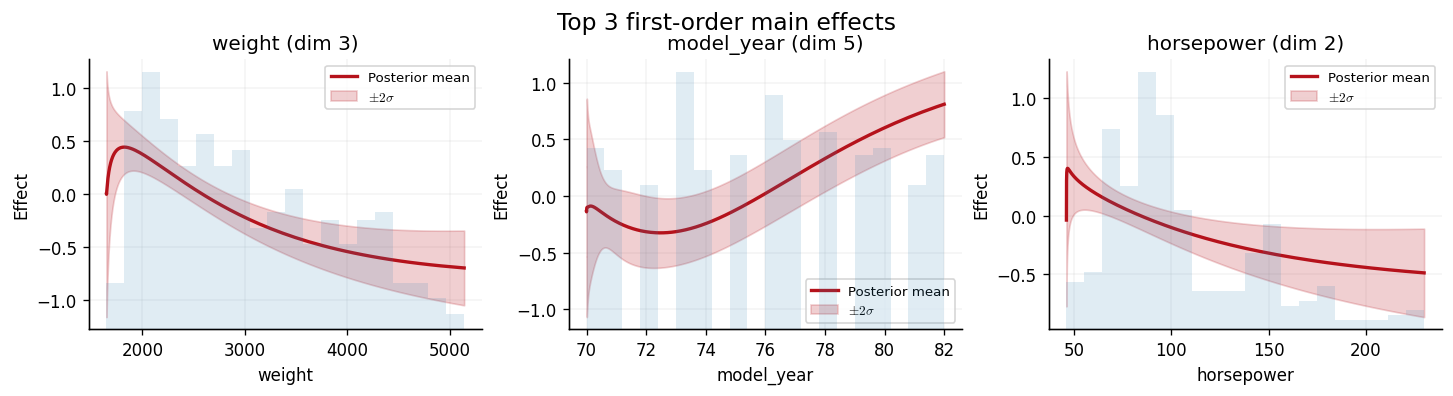
Each panel shows how the OAK model attributes predictive variation to individual features. Features with large, clearly non-zero effects are those that the model identifies as important for predicting fuel consumption. The uncertainty bands widen in regions where training data are sparse, reflecting the GP's epistemic uncertainty.
System configuration
Author: Thomas Pinder
Last updated: Thu, 05 Mar 2026
Python implementation: CPython
Python version : 3.11.14
IPython version : 9.9.0
gpjax : 0.13.6
jax : 0.9.0
jaxtyping : 0.3.6
matplotlib: 3.10.8
numpy : 2.4.1
ucimlrepo : 0.0.7
Watermark: 2.6.0